OPTIMAL INTERMITTENT NAVIGATION
The dung beetle dance

Motivation
Animals use a combination of egocentric navigation driven by the internal integration of environmental cues, interspersed with geocentric course correction and reorientation. These processes are accompanied by uncertainty in sensory acquisition of information, planning and execution. We were inspired by observations of dung beetle navigational strategies that show switching between geocentric and egocentric strategies.
Foraging beetles look for nutrient-rich dung, and then attempt to roll a dung ball along a straight path radially away from the pile [1] with the aim of providing food for their brood. Beetles acquire navigation information using a variety of long-range cues before initiating a roll, and then push the dung ball while walking backwards with their hind legs. Still, they are able to maintain a consistent bearing. They do by performing the the dung beetle 'dance':
Model
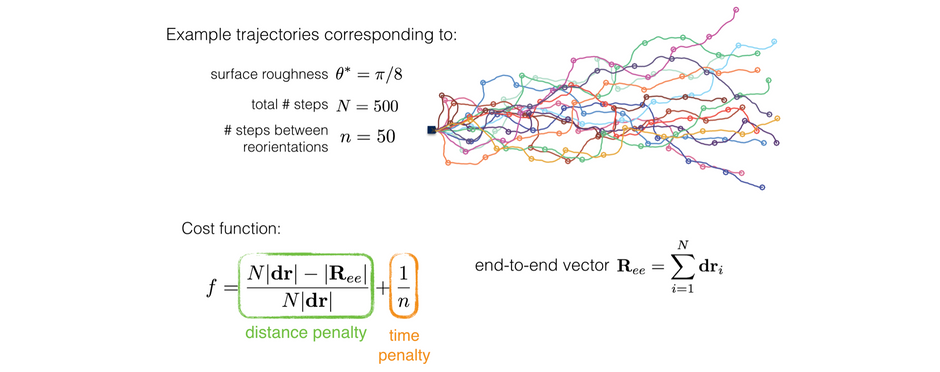
If the beetles stops to reorient often, it would have a straight trajectory but would loose a lot of time; vice verse, if the beetle don't stop to reorient, it might deviate significantly from its intended trajectory.
How often should the beetle stop to reorient, on a specific surface roughness?
To answer this question, we consider an agent moving along a preferred direction in the presence of multiple sources of noise. We address this using a model of a correlated random walk at short time scales that is punctuated by reorientation events leading to a biased random walks at long time scales. This allows us to identify optimal alternation schemes and characterize their robustness in the context of noisy sensory acquisition as well as performance errors linked with variations in environmental conditions and agent–environment interactions.

This allows us to identify optimal alternation schemes and characterize their robustness in the context of noisy sensory acquisition as well as performance errors linked with variations in environmental conditions and agent–environment interactions.
Optimal reorientation intervals
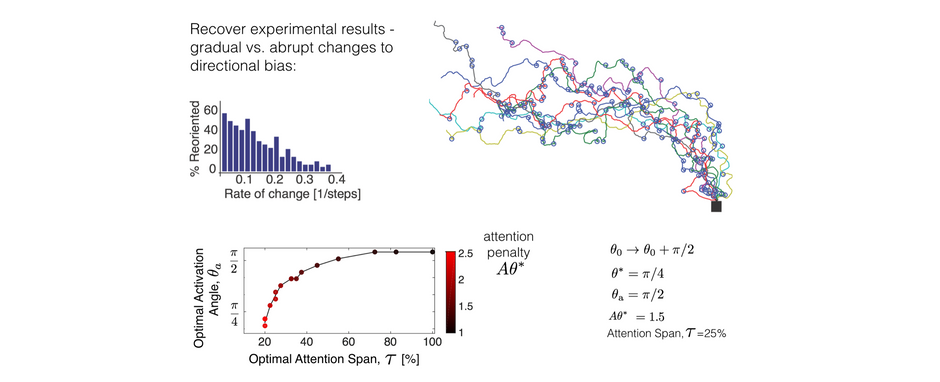
In the simplest setting, we find that the optimal reorientation interval is inversely proportional to the environmental noise and is invariant to sensory acquisition noise. In more complex settings, our study highlights the variations in the optimal navigation strategy that balances accuracy, speed and effort.

What triggers reorientation?
Having understood this simple scenario, we now go back to address the complexities associated with noise in acquisition, planning and execution, in addition to the noise in the turning angle distribution θ*. To address this, we use numerical simulations with the acquisition error ϵd≠0, the error amplification associated with attention A>1, and ask how the agent must optimize the attention span τ≠1 and the threshold activation angle for reorientation θa to minimize the cost
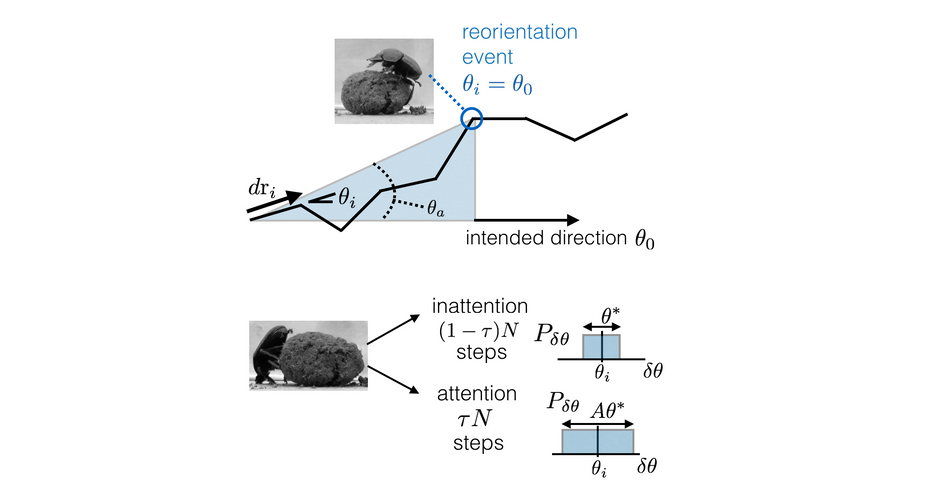
We use the covariance matrix adaptation algorithm (CMA–ES) to determine the optimal strategy, where given a set (θ*,A,ϵd), we determine the optimal set (θa,τ). The CMA-ES is a stochastic derivative-free optimization method for nonlinear or non-convex continuous optimization problems.